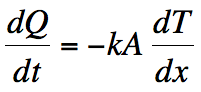Free food.
I woke up yesterday, and as I do everyday, I checked my email. There I saw that I had been tagged on FaceBook by Steve, a relative of mine. He posted the following:
Need some help from my academia family and friends! I need to present "in layman terms" how cold it would have to be outside to freeze 2 gallons of water @ -19ºC.
Background: The product I sell has a moisture cured urethane in it and is activated by water. I am working in Canada where the lowest ever temp recorded was -60ºC (1947) so how long would it take to freeze a 2 gallon sprayer of room temp water which is about 10ºC at -19ºC.
1st person that can explain it (so my block head can understand it) win's a perfectly smoked brisket delivered or shipped to "His or Her" home!!
Now he posted this at 5 am (7am Texas time), and I was still blissfully asleep. One and a half hours later, he wrote
So far my simple question is still unanswered! (Tick Tock) BTW when the west coast awakens my family physicist Vann Priest will have no problem with this so you all had better hurry!!
 |
| CREDIT: Steve |
By the time I awoke at 8:30, Steve had already gotten some really good answers from Brian and Karen, so I was afraid I lost a chance at some Texas smoked brisket. I should make clear that Steve has this awful habit of posting his BBQ on FaceBook, and whenever he does, I drool all over my shirt. However, since he didn’t yet award it officially, I figured I might still have a chance.
 |
| CREDIT: Steve |
A brief shout-out to Kevin who is quite an accomplished smoker. Kevin's brisket is also scrumdiddlyumptious, and I have been privileged to taste it on several occasions. It might be awhile before Kevin or I get another brisket though. He just became the father of twin boys.
So here’s my answer.
First the water has to cool to 0ºC. Newton’s law of cooling states that the rate at which the temperature of an object changes is proportional to the difference in temperature between the object and the environment. Fancy way of saying that if you want to cool something off really quickly, you put it in the refrigerator; if not, leave it in the kitchen.
Mathematically, Newton’s law is written
T is the temperature, t is time, TE is the temperature of the environment, and k is some constant. This is a straightforward first order differential equation. The solution is
The problem though is that to find the time t we need to know both constants, k and C. There’s a lot of complicated physics that goes into k and C; however, to find C, we can set the time equal to zero. We know the initial temperature of the water and the environmental temperature. Punching a few numbers into my handy calculator gives me 3.37. We could do something similar to find k, but we would need to know the temperature of the water sometime later. I don’t have that information, so I can’t find the time it takes to cool down to freezing.
I’m not going to let that stop the analysis though. Once the water reaches 0ºC, it begins to turn into ice. The temperature stays at zero until all the water freezes. We can find how long it takes by knowing that the energy transfer happens by thermal conduction. Here’s the equation governing this phenomenon.
Q is the amount of energy that is being transferred (usually called heat), t is again the time, T is the temperature of the object through which the energy is being transferred, and x refers to the thickness of the object. There are two constants here too. A is the cross-sectional area of the object, and k (a different k) is called the thermal conductivity. (Once again, a lot of complicated physics rolled into a single number).
Here is a major complication. I can look up the thermal conductivity and figure out the area and the thickness. The total amount of energy transferred in so problem; Q = mL where m is the mass of the water and L is the amount of energy required to change the state of the water per kilogram. But this differential equation is for one dimension only. To do it in all three directions is some tough mathematics.
There’s no easy way to solve Steve’s problem.
Or is there?
I’m an experimental physicist. Let’s do the experiment. The freezer in most refrigerators is about -19ºC. Let’s put one gallon of water in the freezer and see how long it takes. The time it takes for 2 gal will be about twice as long.
Two hours into the experiment and the first thin layer of ice begins to form. In another hour, there’s a significant amount of ice. So Steve has about four hours before he needs to worry, and a Texas smoked brisket is on its way to California.